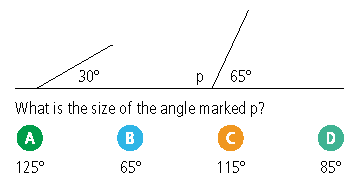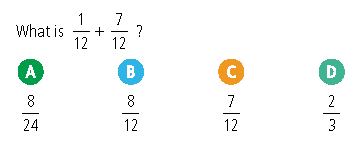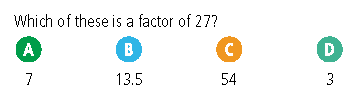I am going to start with a rather big claim: asking and responding to diagnostic questions is the single most important thing I do every lesson. This article will be my attempt to convince you why.
For 13 years, I have taught math (or “maths,” as I like to call it) to students ages 11 to 18 in the United Kingdom. For much of my career, I did not reflect on why I was doing the things I did. I was a relatively successful teacher, whose students always got decent results and seemed to enjoy their lessons, and that was good enough for me. It was only when I started my Mr Barton Maths Podcast that my cozy little world began to crumble. Interviewing educators from around the world really made me stop and question practices that I had done for many years without really thinking about them. These conversations led to two years of reading hundreds of books and research articles; trying, failing, and tweaking new ideas with my students; and eventually writing a book: How I Wish I’d Taught Maths: Lessons Learned from Research, Conversations with Experts, and 12 Years of Mistakes.
One of those key mistakes I made was to ignore the immense power of formative assessment.
Formative assessment is a phrase that is bandied around a lot. It is something all teachers are told we have to do, but often without any real substance or conviction. It is marketed as a generic teaching strategy—one that can be used across all subjects—and so it is usually accompanied by whole-school training sessions, where us mathematics teachers are presented with examples from English, history, and geography and persuaded that they will definitely work for the likes of equations, percentages, and histograms.
So for much of my career, I steered clear of any mention of formative assessment. Then I came across the work of Dylan Wiliam, an expert on the topic. And it is a good thing I did, because I am now convinced that teaching without formative assessment is like painting with your eyes closed.
In 2016, Wiliam sent the following tweet: “Example of really big mistake: calling formative assessment ‘formative assessment’ rather than something like ‘responsive teaching.’ ”
Indeed, “responsive teaching” feels like a much better description to attach to the tools and strategies I will discuss here. The word “assessment” conjures up visions of tests and grades. For teachers, it means more work, and for students, more pressure. While it’s important to see tests as tools of learning, the association with assessment has probably not helped the development and adoption of this most valuable of strategies.
Paul Black, a prominent researcher on formative assessment, and Wiliam explain that an assessment functions formatively “to the extent that evidence about student achievement is elicited, interpreted, and used by teachers, learners, or their peers, to make decisions about the next steps in instruction that are likely to be better, or better founded, than the decisions they would have taken in the absence of the evidence that was elicited.”1
Others define formative assessment as “the process used by teachers and students to recognize and respond to student learning in order to enhance that learning, during the learning.”2
Wiliam makes the point that any assessment can be formative, and that assessment functions formatively when it improves the instructional decisions that are made by teachers, learners, or their peers.3
For me, formative assessment is all about responding in the moment. It is about gathering as much accurate information about students’ understanding as possible in the most efficient way possible, and making decisions based on that. In short, it is about adapting our teaching to meet the needs of our students.
Classroom Culture
If students are afraid of making mistakes, how can we learn from their misunderstandings?
We have probably all taught students who leave questions out in tests and homework for fear of being wrong, and we all know that such actions make it incredibly difficult to help them, as we have no indication of how much or in what areas their understanding is lacking. However, in my experience, far more common is a fear of making mistakes away from the written page. Many formative assessment strategies—and indeed the one I am going to focus on here—require students to be public about their answers, displaying their thoughts in front of their teacher and peers in the moment. If students fear making mistakes, and the consequences of those mistakes, then it is highly likely that they will fail to provide us with any useful information at all. After all, for the child who fears failure, not giving a response is far less daunting than having a go.
So how do we create a classroom culture that helps students overcome this problem?
By ensuring that the questions we ask students are seen not as tools of assessment but as tools of learning. We can only hope to achieve this if there are no negative consequences for being wrong. We can do this by not grading or recording students’ responses to the formative assessment questions we ask in class, for the presence of a grade or record puts a premium upon success, and they are not needed to inform our decisions in the moment.
There also must be positive consequences for honest participation; mistakes need to be embraced as learning opportunities. I know that sounds ridiculously clichéd, but it is true.
Students opting out
Another factor that can render any assessment strategy—but in particular classroom-based formative assessment—limp and ineffective is the classic opt-out. Some students may choose not to give an answer not for fear of being wrong but, to put it bluntly, because they don’t want to think. A shrug, an utterance of “I don’t know,” or a wall of silence tells us absolutely nothing about a student’s understanding of a given concept, and thus leaves us powerless to help.
Allowing such a response also conveys the message that nonparticipation is absolutely fine.
Wiliam argues that engaging in classroom discussion really does make students smarter.4 So, when teachers allow students to choose whether to participate or not—for example, by allowing them to raise their hands to show they have an answer, or settling for a lack of response—we are actually making the achievement gap worse, because those who are participating are getting smarter, while those avoiding engagement are forgoing the opportunities to increase their ability.
Finding comfort in one correct answer
Directly related to students themselves opting out is a common practice among teachers (myself very much included) that essentially does the student’s job of opting out for them. See if this scenario rings any bells:
Me: So, does anyone know what -5 - -2 is?
(Three hands go up, one of which is Josie. Josie always gets everything right.)
Me: Josie, go for it.
Josie: -3, sir.
Me: And why is that, Josie?
Josie: Because subtracting a minus is the same as adding a positive, and negative 5 plus 2 gives you negative 3.
Me: Loving your work as ever, Josie. OK, let’s move on.
Well, that is exactly how many of my early attempts to assess the understanding of my students proceeded. In one book on formative assessment, a teacher is quoted as describing such a scenario as “a small discussion group surrounded by many sleepy onlookers.”5 Likewise, when I interviewed Wiliam for my podcast and asked him to describe an approach in the classroom that he doesn’t think is effective, he replied: “Teachers making decisions about the learning needs of 30 students based on the responses of confident volunteers.” Rarely have truer words been spoken. I find solace in the fact that I am not alone. Wiliam himself describes a similar experience:
When I was teaching full-time, the question that I put to myself most often was: “Do I need to go over this point one more time or can I move on to the next thing?” I made the decision the same way that most teachers do. I came up with a question there and then, and asked the class. Typically, about six students raised their hands, and I would select one of them to respond. If they gave a correct response, I would say “good” and move on.6
One of professor Robert Coe’s “poor proxies for learning” is “(at least some) students have supplied correct answers,” and it is easy to see why.7 I am seeking comfort in one correct answer. When Josie once again produces a perfect answer and a lovely explanation, I make two implicit assumptions: first, that this is down to my wonderful teaching; and second, that every other child in the class has understood the concept to a similar level. But, of course, I have no way of knowing that. By essentially opting out the rest of the class, the only information I am left with concerns Josie.
There are ways around this. We can use popsicle sticks or other random name generators to ensure each student has an equal chance of being selected. These adaptations certainly improve my initial process, but they suffer from the same fatal flaw. All students are not required to participate to the same degree, and so the only student’s understanding I have anything resembling reliable evidence about is the student answering the question. Researcher Barak Rosenshine’s third principle of instruction is: “Ask a large number of questions and check the responses of all students.”8 In the past, I often failed to do that. However, the strategy involving diagnostic questions that I am going to outline below has the full participation of each and every student, along with an explicit use of mistakes, built in to its very core.
What Is a Diagnostic Question?
I used to believe two things that fundamentally dictated how I asked students questions and offered them support:
- For any given question, there were two groups of students: those who could do it and those who could not. Those who could do it were fine to get on with the next challenge, and those who could not needed help. Crucially, they needed the same help.
- Closed questions are bad, and open questions are good. Closed questions encourage a short response, whereas open-ended questions demand much greater depth of thought. Hence, I spent many years fighting the urge to ask students closed questions in class, and instead opted almost exclusively for things like, “Why do we need to ensure the denominators are the same when adding two fractions?” or “How would you convince someone that 3/7 is bigger than 4/11?”
I will return to the first belief in due course, but first let’s deal with the nature of questions.
These two fraction questions are certainly important questions to ask students. But if our aim is to quickly and accurately assess whole-class understanding so we are able to make an informed decision on how to proceed with the lesson, they are not so good.
Their strength is their weakness. The fact that they encourage students to think, take time to articulate, and provoke discussion and disagreement makes them entirely unsuitable for effective formative assessment. How would we go about collecting and assessing the responses to “Why do we need to ensure the denominators are the same when adding two fractions?” from 30 students in the middle of a lesson as a means of deciding whether the class is ready to move on?
Open-ended questions like these are great for homework, tests, extension activities, and lots of other different situations. However, they are not great for a model of responsive teaching.
Nor is it the case that closed questions prevent thinking. Wiliam gives the example of asking if a triangle can have two right angles.9 This is about as closed a question as you can get—the answer is either yes or no. But the thinking involved to get to one of those answers is potentially very deep indeed. Students may consider whether it is possible to have an angle measuring 0 degrees, or if parallel lines will meet at infinity. But this closed question, while it is indeed a brilliant one, is equally unsuited for a model of responsive teaching. If a particular student answered no, would we be convinced that he understood the properties of triangles and angles fully? Or has he just guessed? Without further probing, it is impossible to tell, and hence we are back to the same issues we have with the more open-ended fraction questions above.
So, if open-ended questions are unsuitable for this style of formative assessment, and not all closed questions are suitable, then what questions are left?
Step-forward diagnostic multiple-choice questions, or just diagnostic questions, as I refer to them.
Diagnostic questions are designed to help identify and, crucially, understand students’ mistakes and misconceptions in an efficient and accurate manner. Mistakes tend to be one-off events—the student understands the concept or the algorithm, but may make a computational error due to carelessness or cognitive overload. Give students the same question again, and they are unlikely to make the same mistake; inform the students that they have made a mistake somewhere in their work, and they are likely to be able to find it. Misconceptions, on the other hand, are the result of erroneous beliefs or incomplete knowledge. The same misconception is likely to occur time and time again. Informing the students who have made an error due to a misconception is likely to be a waste of time, as, by definition, they do not even know they are wrong. Good diagnostic questions can help you identify and understand both mistakes and misconceptions.
The best way to explain a diagnostic question is to show you one:
Answer A may suggest that the student understands that angles on a straight line must add up to 180 degrees, and that the student is able to identify the relevant angle, but that he has made a common arithmetic error when subtracting 65 from 180.
Answer B may be the result of students muddling up their angle facts, mistakenly thinking this is an example of vertically opposite angles being equal.
Answer C is the correct answer.
Answer D may imply that the student is aware of the concept that angles on a straight line must add up to 180 degrees, but that the student has included all visible angles in her calculations.
Notice how each of these answers reveals a specific and different mistake or misconception. Imagine you had a group of students who answered A, another group who answered B, and a final group who answered D. Would all three groups require the same intervention from you, their teacher?
I don’t think so. Which brings us to my second (erroneous) belief. It is not always the case that students either can or cannot answer a question correctly. Sure, there may be some students who get the question correct for the same or similar reasons. But there are likely to be students who get a question wrong for very different reasons, and it is the reason they get the question wrong that determines the specific type of intervention and support they require.
For example, students who answered B and D may benefit from an interactive demonstration (for example, using GeoGebra) to illustrate the relationship between angles on a straight line. Students who chose B could then be presented with an exercise where they are challenged to match up an assortment of diagrams with the angle fact they represent. Those who selected D may benefit more from a selection of examples and nonexamples of angles on a straight line. But what about students who answered A? Their problem lies not with the relationship between the angles, but with their mental or written arithmetic. This may be a careless mistake, or it may be an indication of a more serious misconception with their technique for subtraction. Either way, it is not a problem that is likely to be solved by giving these students the same kind of intervention as everyone else. However you choose to deal with these students, there is little doubt that there is an advantage to knowing not just which students are wrong, but why they are wrong. And I have never come across a more efficient and accurate way of ascertaining this than by asking a diagnostic question.
So, what makes a question a diagnostic question? For the way I define and use them, there needs to be one correct answer and three incorrect answers, and each incorrect answer must reveal a specific mistake or misconception. I can—and indeed do—ask students for the reasons for their answers, but I should not need to. If the question is designed well enough, then I should gain reliable evidence about my students’ understanding without having to have further discussion.
What Makes a Good Diagnostic Question?
Not all diagnostic questions are born equal, and writing a good one is hard. Indeed, the more I use diagnostic questions with my students and colleagues, the more I read about misconceptions in mathematics, and the more experience I get in writing them, the harder I am finding it! I take some solace from the fact that this could very well be the Dunning-Kruger effect10 playing out, in that as I grow more knowledgeable, I am also more aware of the difficulty of the challenge as well as my own considerable deficiencies.
At the time of writing, I have written around 3,000 diagnostic multiple-choice questions for mathematics. The vast majority of these I have used with my students either in the classroom or as part of an online quiz on my Diagnostic Questions platform,* and many have been tweaked, adjusted, and binned over the years. Throughout that time, and inspired by the work of Caroline Wylie and Wiliam,11 I have devised a series of golden rules for what makes a good diagnostic question:
Golden Rule 1: It should be clear and unambiguous.
We all have seen badly worded questions in exams and textbooks, but with diagnostic questions, sometimes the ambiguity can be in the answers themselves. Consider the following question:
Golden Rule 2: It should test a single skill/concept.
Many good questions test multiple skills and concepts. Indeed, a really effective way to interleave,† which is where topics are studied in short bursts with frequent switching (as opposed to presented in blocks), is to combine multiple skills and concepts together within a single question. But good diagnostic questions should not do this. The purpose of a diagnostic question is to home in on the precise area that a student is struggling with and provide information about the precise nature of that struggle. If there are too many skills or concepts involved, then the accuracy of the diagnosis invariably suffers.
Golden Rule 3: Students should be able to answer it in less than 10 seconds.
This is directly related to Golden Rule 2. If students are spending more than 10 seconds thinking about the answer to a question, the chances are that more than one skill or concept is involved, which makes it hard to determine the precise nature of any misconception they may hold.
Golden Rule 4: You should learn something from each incorrect response without the student needing to explain.
A key feature that distinguishes diagnostic multiple-choice questions from nondiagnostic multiple-choice questions is that the incorrect answers have been chosen very, very carefully in order to reveal specific misconceptions. In fact, they are often described as distractors, although I do not like this term, as it implies they are trick answers. The key point is that if a student chooses one of these answers, it should tell you something.
Golden Rule 5: It cannot be answered correctly while still holding a key misconception.
This is the big one. For me, it is the hardest skill to get right when writing and choosing questions, but also the most important. We need to be sure that the information and evidence we are receiving from our students is as accurate as possible, and in some instances that is simply not the case.
Consider the following question:
Or am I? If I am going to use this question in class, presumably my purpose is something along the lines of assessing if students have a good understanding of multiples. And yet, something that is not assessed at all in this question is arguably the biggest misconception students have with the topic.
Imagine you are a student coming into your math lesson and you are told that today you are studying multiples. Oh no, you think, I always get multiples and factors muddled up—I can never remember which ones are the bigger numbers. And then you are presented with the question above, and a smile appears on your face. You can get this question correct without knowing the difference between factors and multiples, as there are no factors present. And if I am your teacher, and several of your peers have the same problem, it could well be the case that you all get this question correct and I conclude that you understand factors and multiples, without ever testing to see if you can distinguish between the two concepts.
Interestingly, by presenting my students with this question, they may subsequently infer that multiples are “the bigger numbers” due to the absence of any number smaller than 6, and hence may learn the difference between factors and multiples indirectly that way. However, this is something I would prefer to assess directly, especially if I am trying to discern in the moment if I have enough evidence to move on.
So, a better question might be something like this:
Seeing as I make such extensive use of diagnostic questions, I want to ensure that the information I receive back from my students’ answers is as accurate and valid as possible. Hence, putting such time into the creation and selection of good questions is time well spent.
So, that is why I am more than a little obsessed with formative assessment, and my favorite tools for delivering it are high-quality diagnostic multiple-choice questions.
But how do I collect my students’ responses? In the past, I would have messed around with electronic voting devices. But all it takes is an empty battery, a dodgy Wi-Fi signal, or a mischievous child, and your lesson can quickly be skidding off the rails. Mini-whiteboards too, while great for students writing down their work, fall prey to faulty pens and an apparently unavoidable adolescent urge to draw something not exactly related to the content of the lesson. No, once again I defer to Wiliam, who, when I interviewed him for my Mr Barton Maths Podcast, advised that students should vote with their fingers, because, as he said, students may forget to bring a pen to a lesson, but they rarely forget their fingers.
So, at the start of each lesson, I project a diagnostic question on my board. I ask students to consider the answer in silence. I then count down from three and ask them to raise their hand high in the air, showing one finger for A, two for B, three for C, and four for D. Quickly, I am able to get a picture of their understanding. I then ask a student who has chosen A to explain his reasoning, then a student who has chosen B, and so on. At the end of this process, we have a revote, and then—because there is a danger that students are just copying the perceived cleverest student in the class—I ask a follow-up question that tests the same skill. Once my students are used to this routine, it takes around two minutes per question, and I always ask at least three questions per lesson. And if some students are still struggling after the follow-up question, I am able to help them over the course of the lesson.
Which brings me to the final reason why I love diagnostic questions so much: the ability to plan for error. In the past, I would often find myself on the receiving end of a completely unexpected answer, while standing in front of a sea of 30 confused faces all looking to me for help. I would be forced to think on the spot—attempting to diagnose the error and think of a way of helping resolve it, all while trying to juggle the hundreds of other considerations tumbling through a teacher’s mind in the middle of a lesson. Now, I do not need to. By using diagnostic questions and studying the wrong answers in advance, I can plan for these errors, ensuring I have explanations, resources, and strategies ready to help. My thinking can be done before the lesson, thus making me much more effective during the lesson.
I love good diagnostic questions. I know of no more accurate, efficient way of getting a sense of my students’ understanding of a concept, and then adjusting my teaching to meet their needs.
Craig Barton has taught math to secondary school students in the United Kingdom for 13 years. He is the creator of the websites www.mrbartonmaths.com, which offers free math support and resources to teachers and students, and www.diagnosticquestions.com, which contains the world’s largest collection of free diagnostic multiple-choice math questions. He is also the host of Mr Barton Maths Podcast, which features interviews with inspiring figures in education. This article is adapted with permission from his book, How I Wish I’d Taught Maths: Lessons Learned from Research, Conversations with Experts, and 12 Years of Mistakes (John Catt Educational, 2018).
*Diagnostic Questions is a free formative assessment platform that contains more than 40,000 diagnostic multiple-choice math questions suitable for students ages 4 to 18. Questions can be used in the classroom to identify misconceptions and promote discussion, or can be used as quizzes through the platform, which immediately returns the results back to the teacher with actionable insights into the students’ understanding. To access these questions, visit www.diagnosticquestions.com. (back to the article)
†For more on the practice of interleaving, see “Strengthening the Student Toolbox” in the Fall 2013 issue of American Educator. (back to the article)
Endnotes
1. Paul Black and Dylan Wiliam, “Developing a Theory of Formative Assessment,” Educational Assessment, Evaluation and Accountability 21 (2009): 9.
2. Bronwen Cowie and Beverley Bell, “A Model of Formative Assessment in Science Education,” Assessment in Education: Principles, Policy & Practice 6 (1999): 101–116.
3. Dylan Wiliam, Embedded Formative Assessment (Bloomington, IN: Solution Tree Press, 2011).
4. Wiliam, Embedded Formative Assessment.
5. Paul Black et al., Assessment for Learning: Putting It into Practice (Maidenhead, UK: Open University Press, 2003), 32.
6. Dylan Wiliam, “The 9 Things Every Teacher Should Know,” TES, September 2, 2016, www.tes.com/us/news/breaking-views/9-things-every-teacher-should-know.
7. Robert Coe, “Improving Education: A Triumph of Hope over Experience” (lecture, Durham University, Durham, UK, June 18, 2013), www.cem.org/attachments/publications/ImprovingEducation2013.pdf.
8. Barak Rosenshine, “Principles of Instruction: Research-Based Strategies That All Teachers Should Know,” American Educator 36, no. 1 (Spring 2012): 12.
9. Wiliam, Embedded Formative Assessment.
10. See Justin Kruger and David Dunning, “Unskilled and Unaware of It: How Difficulties in Recognizing One’s Own Incompetence Lead to Inflated Self-Assessments,” Journal of Personality and Social Psychology 77 (1999): 1121–1134.
11. Caroline Wylie and Dylan Wiliam, “Diagnostic Questions: Is There Value in Just One?” (paper presentation, American Educational Research Association annual meeting, San Francisco, CA, April 11, 2006), www.mrbartonmaths.com/resourcesnew/8.%20Research/Formative%20Assessment…; and Wiliam, Embedded Formative Assessment.