Everybody wants teachers to be knowledgeable. Yet there is little agreement on exactly what kinds of knowledge are most important for teachers to possess. Should teachers have deep knowledge of the subject matter they are teaching, gleaned from college study, additional graduate courses, or even research experience? Do they need to understand how students typically think when they approach a problem or theory? Is there some optimal combination of these different types of knowledge?
Researchers have long speculated that a teacher’s knowledge of common student misconceptions could be crucial to student learning.1 This view recognizes that learning is as much about unlearning old ideas as it is about learning new ones.2 Learners often find it difficult to change their misconceptions, since these are ideas that make sense to them. Some researchers advocate, therefore, that teachers should know common student misconceptions for the topics that they teach,3 and others suggest that teachers interview4 or test5 their students to reveal student preconceptions early on in the learning process. Yet the research falls short in assessing teachers’ knowledge of particular student misconceptions and the actual impact of this knowledge on student learning.
Such discussions as these, if they use data at all, are often based on indirect methods of gauging teacher knowledge. College degrees earned, courses taken, and grades achieved often serve as proxies for a teacher’s subject-matter knowledge, which is identified as the general conceptual understanding of a subject area possessed by a teacher.6 But studies that rigorously investigate the relationship between the different kinds of teacher knowledge and student gains in understanding are rare.7
We set out to better understand the relationship between teacher knowledge of science, specifically, and student learning.8 We administered identical multiple-choice assessment items both to teachers of middle school physical science (which covers basic topics in physics and chemistry) and to their students throughout the school year. Many of the questions required a choice between accepted scientific concepts and common misconceptions that have been well documented in the science education literature.9 We also asked the teachers to identify which wrong answer they thought students were most likely to select as being correct. Through a student posttest at the end of the school year, we were able to study the impact on student learning of teacher knowledge of science and the accuracy of their predictions of where students are likely to have misconceptions.
Not all items had very popular wrong answers, but for those that did (12 items of the 20, or 60 percent), we found that teachers who could identify these misconceptions had larger classroom achievement gains, much larger than if teachers knew only the correct answers. This finding suggests that a teacher’s ability to identify students’ most common wrong answer on multiple-choice items, a form of pedagogical content knowledge, is an additional measure of science teacher effectiveness. For items on which students generally had no popular misconceptions, teacher subject-matter knowledge alone accounted for higher student gains.
Our Study
The goal of our study was to test two hypotheses regarding teacher knowledge in middle school physical science courses:
Hypothesis 1: Teachers’ knowledge of a particular science concept that they are teaching predicts student gains on that concept.
Hypothesis 2: Teachers’ knowledge of the common student misconceptions related to a particular science concept that they are teaching predicts student gains on that concept.
We assessed teachers’ subject-matter knowledge and their knowledge of students’ misconceptions in the context of the key concepts defined by the National Research Council’s (NRC) National Science Education Standards and measured their relationship to student learning.* We administered the same multiple-choice items to both students and teachers. And we asked teachers to identify the incorrect item (that is, the student misconception) that they believed students would most often select in lieu of the correct answer. This method allowed us to simultaneously evaluate the teachers’ knowledge of both subject matter and students’ misconceptions and examine if these teacher measures predict student gains in middle school physical science classrooms.
Science learners often struggle with misconceptions, and multiple-choice tests function well in diagnosing popular misconceptions that can impede the learning of science concepts.10 Good examples include the causes of the seasons and of the phases of the moon. For instance, a particularly common view, often held by adults, is that the seasons are caused by the earth’s elliptical orbit rather than the changing angle of the sun’s rays hitting the surface of the earth. In the documentary A Private Universe, bright and articulate graduating college seniors, some with science majors, revealed their misunderstandings of such common middle school science topics.11 If teachers hold such misconceptions themselves or simply are unaware that their students have such ideas, their attempts to teach important concepts may be compromised.
We measured gains on key concepts during a one-year middle school physical science course. As is common in this type of research, we controlled for differences in student demographics, such as race, ethnicity, home language spoken, and parents’ education. By using individual test items, we could assess how strongly teachers’ subject-matter knowledge and knowledge of students’ misconceptions were associated with student gains.
Our study design was also able to account for the amount of physical science content taught during the middle school years, which can vary greatly. While some schools devote an entire academic year to the subject, other schools include physical science within a general science sequence that covers earth and space science and life science. Also, we were concerned that the initial science achievement of participating classrooms might obscure any changes in student achievement during the school year. For example, it may be that, compared with their less experienced colleagues, more experienced or expert teachers were assigned students who have shown higher prior achievement. Administering a pretest, a midyear test, and a posttest enabled us to control for students’ baseline knowledge level.
Our initial nationwide recruitment effort yielded 620 teachers of seventh- and eighth-grade physical science at 589 schools (91 percent of which were public). Of the teachers who at first volunteered to be part of this study, 219 followed through. They were quite experienced, with a mean time teaching of 15.6 years and a mean time teaching middle school physical science of 10.4 years. They had a range of undergraduate preparation: 17 percent had a degree in the physical sciences; 25 percent, a degree in another science; 36 percent, a science education degree; 23 percent, an education degree in an area other than science; and 9 percent, a degree in another field. Multiple undergraduate degrees were held by 8 percent of teachers. Of the total sample, 56 percent held a graduate degree in education and 14 percent held a graduate degree in science.
In return for their participation, we offered to report back to teachers the aggregate scores of their students and the associated student gains in comparison with our national sample.12 Seventy-eight percent of the students were in eighth grade, while 22 percent were in seventh grade. At the end, we obtained usable data from a total of 9,556 students of 181 teachers.
Design Details
For the assessment, we constructed multiple-choice questions13 that reflect the NRC’s physical science content standards for grades 5–8.14 While we are constrained from publishing the actual wording of the 20 questions because the assessment is widely used by professional development programs nationally,15 the assessment addresses three content areas: properties and changes of properties in matter (six questions), motions and forces (five questions), and transfer of energy (nine questions). (See Table 1 for details.)
Multiple-choice questions fell into two categories with respect to the relative popularity of the wrong answers. Eight of the 20 questions had “weak” or no evident misconceptions, with the most common wrong answer chosen by fewer than half of the students who gave incorrect responses. Consider the results for Sample Item 1 (shown below), for example. While 38 percent of students answered this question correctly (option d), a corresponding 62 percent answered incorrectly, with 42 percent of those who were incorrect selecting option b. While option b was the most popular wrong answer, it was not chosen by more than half of the students who answered incorrectly, so the item is considered not to have an identifiable misconception.
1. A scientist is doing experiments with mercury. He heats up some mercury until it turns into a gas. Which of the following do you agree with most?
A total of 12 questions had “strong” misconceptions, meaning 50 percent or more of students who chose a wrong answer preferred one particular distractor. For example, as shown in Sample Item 2, only 17 percent of students answered the question correctly (option a), and a corresponding 83 percent answered incorrectly. A very large fraction (59 percent) of students chose one particular wrong answer, option d; of the students choosing an incorrect answer, 71 percent preferred this single distractor. This response indicates a strong misconception.
2. Eric is watching a burning candle very carefully. After all of the candle has burned, he wonders what happened to the wax. He has a number of ideas; which one do you agree with most?
Classroom coverage of the content represented by the test items was near universal. Only eight teachers reported that they did not cover the content tested by one particular item, and two teachers reported that they did not cover the content in two items.
In Table 1, we break down by standard the broad concepts addressed by the 20 test items, with their common misconceptions noted in italics underneath each one. Relevant earlier studies about these specific student misconceptions are cited in the endnotes.
On the midyear and end-of-year assessments, we included four nonscience questions—two reading and two mathematics—to get a general sense of students’ engagement in and effort on the tests themselves. The two reading questions were constructed to represent students’ comprehension of a science-related text. The first of these required the students to comprehend the actual text, while the second required them to infer from the text. Similarly, of the two mathematics questions, one required a well-defined arithmetic operation, while the second required students to identify the relevant features of a word problem before responding. Mean reading and math scores were both 58 percent.
These four items were used to construct what is called a composite variable. Students who correctly answered fewer than half of the nonscience content items (27 percent of participants) were tagged as “low nonscience”; those who correctly answered at least 50 percent of the four reading and math items were tagged as “high nonscience.” This index allowed us to examine gains for each group separately. We hypothesized that students who performed in the low-nonscience range in reading and doing simple math would have had difficulty answering the science questions on the test or simply would not have given the test their best effort.
Teacher Subject-Matter Knowledge and Knowledge of Students’ Misconceptions
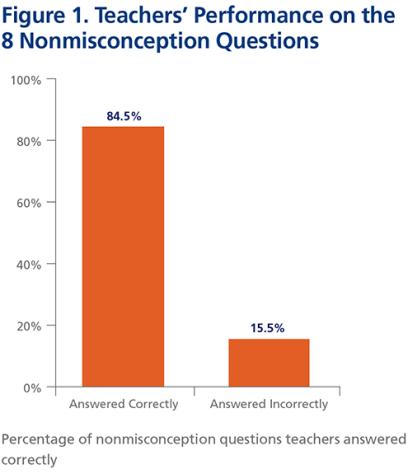
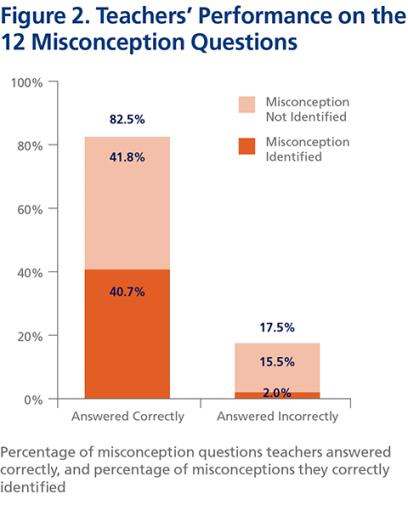
Teacher performance in subject-matter knowledge on the pretest was relatively strong, with 84.5 percent correct on nonmisconception items and 82.5 percent on misconception items. On average, teachers missed three out of 20 items. Teachers’ knowledge of students’ misconceptions—that is, the ability to identify the most common wrong answer on misconception items—was weak, with an average score of 42.7 percent identified. On average, they identified only five out of the 12 items with strong misconceptions.
Teachers’ performance on each of the eight nonmisconception items fell into one of two categories (see Figure 1 below):
- Subject-matter knowledge (teacher answered correctly)—84.5 percent of responses.
- No subject-matter knowledge (teacher answered incorrectly)—15.5 percent of responses.
(click image for larger view)
As expected, the majority of teachers were competent in their subject-matter knowledge, especially when the item did not include a strong misconception among its distractors.
Teachers’ performance on each of the 12 misconception items fell into one of four possible categories (see Figure 2 below):
- Had both subject-matter knowledge and knowledge of students’ misconceptions (teacher answered correctly and knew the most common wrong student answer)—40.7 percent of responses.
- Had subject-matter knowledge, but no knowledge of students’ misconceptions (teacher answered correctly but did not know the most common wrong student answer)—41.8 percent of responses.
- Had no subject-matter knowledge, but had knowledge of students’ misconceptions (teacher answered incorrectly but knew the most common wrong student answer)—2.0 percent of responses.
- Had neither subject-matter knowledge nor knowledge of students’ misconceptions (teacher answered incorrectly and did not know the most common wrong student answer)—15.5 percent of responses.
(click image for larger view)
In the case of teachers not knowing the science (that is, answering the item incorrectly), most selected the dominant student misconception as their own “correct” answer. We decided to combine the third and fourth categories into one, because teachers in both categories did not possess the relevant subject-matter knowledge for that item. Moreover, it is hard to interpret the meaning of the very small (2 percent) category of teachers’ responses that lacked subject-matter knowledge but showed knowledge of students’ misconceptions.
Teacher subject-matter knowledge and knowledge of students’ misconceptions thus appear related, rather than independent from each other.25 Whereas some researchers have argued that there are no formal differences between types of teacher knowledge,26 it seems that subject-matter knowledge, at least in the form that we measured, should be considered a necessary, but not sufficient, precondition of knowledge of students’ misconceptions.
Student Achievement
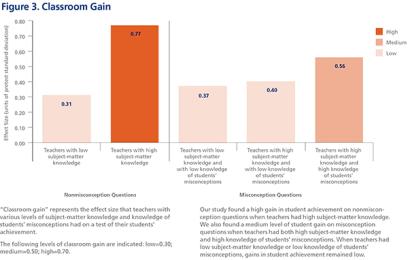
Student scores were relatively low, indicating that the science assessment items were difficult. The mean pretest score across all items (both those without misconceptions and those with misconceptions) was 37.7 percent. Mean scores on the final test were higher at 42.9 percent: 44.8 percent for items without misconceptions and 41.7 percent for those with misconceptions. Students had a slightly easier time learning the content for which there appeared to be no dominant misconception. Our analysis of teacher knowledge at the start of the year shows high levels of subject-matter knowledge, with some weaknesses, and rather moderate levels of knowledge of students’ misconceptions, as measured by teachers’ prediction of the most common wrong answers of their students. Most importantly, we found that student gains are related to teacher knowledge, as shown below in Figure 3. Students made high gains on nonmisconception questions when teachers had high subject-matter knowledge. On misconception questions, students made medium gains if the teachers had both high subject-matter knowledge and high knowledge of misconceptions. In all other constellations, the student gains were low.
(click image for larger view)
In addition, we found interesting differences between high-nonscience and low-nonscience students. The former showed much larger gains than the latter. The high-nonscience students, even if their teacher did not have the requisite subject-matter knowledge and knowledge of students’ misconceptions, made moderate gains. There are many possible explanations for this result. For instance, these students may have found ways to gain knowledge from other sources, such as their textbooks, homework, or discussions with other students.
Having a more knowledgeable teacher is associated with even larger gains for the high-nonscience students than for the low-nonscience students, bringing to mind the so-called Matthew effect, which, loosely stated, says that those with an attribute in abundance (in this case, knowledge) tend to gain more than those who start with less.27 Research has found that students with low reading levels exhibit lower gains in other subjects because much of the effort behind learning requires reading texts.28
It also may be the case that students who answered the embedded reading and mathematics items incorrectly may simply not have taken these questions (or the test as a whole) seriously. Those with low scores on these questions may have gotten these questions wrong because they were uninterested, and their performance on the 20 science items may likewise have suffered. If this is the case, the findings for students of high-nonscience levels (73 percent of the total) should be emphasized as more fairly reflecting the impact of teacher subject-matter knowledge and knowledge of students’ misconceptions.
However, a significant gain was seen on nonmisconception items for low-nonscience students if they had a knowledgeable teacher, so at least some appear to have taken the tests seriously. It also appears that students with low reading and math scores were particularly dependent on the teacher’s subject-matter knowledge, exhibiting no significant gain unless their teachers had the requisite subject-matter knowledge for these items (and the items had no misconceptions). The lack of gain on misconception items for these students, independent of the level of teacher subject-matter knowledge or knowledge of students’ misconceptions, is particularly troubling. These items may simply have been misread, or they may be cognitively too sophisticated for these students, or the students may not have tried their hardest on a low-stakes test.
Among the students with high math and reading scores, our analysis reveals a clear relationship of teacher knowledge to student gains. For nonmisconception items, student gains are nearly double if the teacher knows the correct answer. When items have a strong misconception, students whose teachers have knowledge of students’ misconceptions are likely to gain more than students of teachers who lack this knowledge. Much of what happens in many science classrooms could be considered as simply a demonstration of the teacher’s own subject-matter knowledge, without taking into account the learner’s own subject-matter knowledge. Without teachers’ knowledge of misconceptions relevant to a particular science concept, it appears that their students’ success at learning will be limited.
Notably, “transfer” of teacher subject-matter knowledge or knowledge of students’ misconceptions between concepts appears to be limited. For example, a teacher’s firm grasp of electrical circuits and relevant misconceptions appears to have little to do with the effective teaching of chemical reactions. Teachers who are generally well versed in physical science still may have holes that affect student learning of a particular concept. Our findings suggest that it is important to examine teacher knowledge surrounding particular concepts, because student performance at the item level is associated with teacher knowledge of a particular concept.
Moreover, in teaching concepts for which students have misconceptions, knowledge of students’ ideas may be the critical component that allows teachers to construct effective lessons. Because teachers’ knowledge of students’ misconceptions is low, compared with their knowledge of the science content, professional development focusing on this area could help teachers (and students) substantially.
Subject-matter
knowledge is an important predictor of student learning. The need for teachers to know the concepts they teach may sound like a truism. But while one may assume that the science content of middle school physical science is, in general, well understood by teachers, there are noticeable holes in their knowledge, which differ by teacher. It is not surprising that teachers with the proper subject-matter knowledge of a given concept can achieve larger gains with their students than can those lacking that knowledge; a teacher without subject-matter knowledge may teach the concept incorrectly, and students may end up with the same incorrect belief as their teacher.
Effectiveness of middle school science teachers may thus have more to do with a mastery of all the concepts that they teach than with the depth of their knowledge in any particular topic. The increasing involvement of science professors in teacher professional development could focus those programs too narrowly on the scientists’ special areas of expertise, which might boost participants’ subject-matter knowledge only in a narrow set of topics. Conducting a diagnostic identification and remediation of teachers’ knowledge “holes” might prove more advantageous.
An intriguing finding of this study is that teachers who know their students’ most common misconceptions are more likely to increase their students’ science knowledge than teachers who do not. Having a teacher who knows only the scientific “truth” appears to be insufficient. It is better if a teacher also has a model of how students tend to learn a particular concept, especially if a common belief may make acceptance of the scientific view or model difficult.
This finding, too, has practical implications. In professional development, an emphasis on increasing teachers’ subject-matter knowledge without sufficient attention to the preconceived mental models of middle school students (as well as those of the teachers) may be ineffective in ultimately improving their students’ physical science knowledge.
Philip M. Sadler is the director of the Science Education Department at the Harvard-Smithsonian Center for Astrophysics. His research focuses on assessing students’ scientific misconceptions; the high school-to-college transition of students who pursue science, technology, engineering, and mathematics (STEM) careers; and enhancing the skills of science teachers. Gerhard Sonnert is a research associate at the Harvard-Smithsonian Center for Astrophysics. His research focuses on gender in science, the sociology and history of science, and science education. This article is adapted from Philip M. Sadler, Gerhard Sonnert, Harold P. Coyle, Nancy Cook-Smith, and Jaimie L. Miller, “The Influence of Teachers’ Knowledge on Student Learning in Middle School Physical Science Classrooms,” American Educational Research Journal 50 (2013): 1020–1049. Copyright © 2013 by the American Educational Research Association. Published by permission of SAGE Publications, Inc.
*We conducted our study prior to the advent of the Next Generation Science Standards, for which curricula are not yet widely available. (back to the article)
Endnotes
1. David P. Ausubel, Joseph D. Novak, and Helen Hanesian, Educational Psychology: A Cognitive View, 2nd ed. (New York: Holt, Rinehart and Winston, 1978).
2. Lee S. Shulman, “Those Who Understand: Knowledge Growth in Teaching,” Educational Researcher 15, no. 2 (1986): 4–14. Two other key studies that emphasize the importance of subject-matter teaching and knowledge of common student struggles and errors are Heather C. Hill, Stephen G. Schilling, and Deborah Loewenberg Ball, “Developing Measures of Teachers’ Mathematics Knowledge for Teaching,” Elementary School Journal 105 (2004): 11–30; and Pamela L. Grossman, The Making of a Teacher: Teacher Knowledge and Teacher Education (New York: Teachers College Press, 1990).
3. William S. Carlsen, “Domains of Teacher Knowledge,” in Examining Pedagogical Content Knowledge: The Construct and Its Implications for Science Education, ed. Julie Gess-Newsome and Norman G. Lederman (Boston: Kluwer Academic, 1999), 133–144; and John Loughran, Amanda Berry, and Pamela Mulhall, Understanding and Developing Science Teachers’ Pedagogical Content Knowledge, 2nd ed. (Rotterdam: Sense Publishers, 2012).
4. Eleanor Ruth Duckworth, “The Having of Wonderful Ideas” and Other Essays on Teaching and Learning (New York: Teachers College Press, 1987).
5. David Treagust, “Evaluating Students’ Misconceptions by Means of Diagnostic Multiple Choice Items,” Research in Science Education 16 (1986): 199–207.
6. Shulman, “Those Who Understand.”
7. Jürgen Baumert, Mareike Kunter, Werner Blum, et al., “Teachers’ Mathematical Knowledge, Cognitive Activation in the Classroom, and Student Progress,” American Educational Research Journal 47 (2010): 133–180.
8. Our efforts were part of a National Science Foundation–funded project to produce a set of assessments for diagnostic purposes in middle school classrooms teaching physical science (grants EHR-0454631, EHR-0412382, and EHR-0926272). Any opinions, findings, conclusions, or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
9. Philip M. Sadler, “Psychometric Models of Student Conceptions in Science: Reconciling Qualitative Studies and Distractor-Driven Assessment Instruments,” Journal of Research in Science Teaching 35 (1998): 265–296; Kenneth J. Schoon, “Misconceptions in the Earth and Space Sciences: A Cross-Age Study” (PhD diss., Loyola University of Chicago, 1989); and Treagust, “Evaluating Students’ Misconceptions.”
10. Sadler, “Psychometric Models”; and Treagust, “Evaluating Students’ Misconceptions.”
11. Harvard-Smithsonian Center for Astrophysics, A Private Universe, directed by Matthew H. Schneps and Philip M. Sadler (South Burlington, VT: Annenberg/CPB Project, 1987), VHS videocassette.
12. A few caveats are in order. Our measures of teacher subject-matter knowledge and knowledge of student misconceptions may be proxies for other variables not included. One could imagine, for instance, that years of teaching experience is the key contributor to subject-matter knowledge and knowledge of student misconceptions, and hence student gains. To explore if this might be the case, we investigated models using variables such as teachers’ years of teaching in the classroom and years of teaching physical science, among others. None reached a level of statistical significance when included with measures of subject-matter knowledge and knowledge of student misconceptions. Another consideration is that because participating teachers volunteered to join this project, our results may not be generalizable to other middle school physical science teachers. It may be that our teachers were more confident in their abilities, or eager to participate because they felt their students would perform well. Also, our student sample is not fully representative of the national population: black and Hispanic students are underrepresented, and students with parents who have college degrees are overrepresented. However, the sample was large enough to likely have captured the range of existing variation in the relevant variables studied such that these factors could be controlled for in a hierarchical statistical model.
13. For a description of the process used to create assessment items and instruments in all fields of science, see Philip M. Sadler, Harold Coyle, Jaimie L. Miller, Nancy Cook-Smith, Mary Dussault, and Roy R. Gould, “The Astronomy and Space Science Concept Inventory: Development and Validation of Assessment Instruments Aligned with the K–12 National Science Standards,” Astronomy Education Review 8 (2010): 1–26.
14. Our descriptions of the National Research Council’s standards are adapted from National Academy of Sciences, National Science Education Standards (Washington, DC: National Academy Press, 1996), 154–155.
15. Comparable assessments are available online at www.cfa.harvard.edu/smgphp/mosart.
16. B. R. Andersson, “Some Aspects of Children’s Understanding of Boiling Point,” in Cognitive Development Research in Science and Mathematics: Proceedings of an International Seminar, ed. W. F. Archenhold et al. (Leeds, UK: University of Leeds, 1980), 252–259.
17. Saouma B. BouJaoude, “A Study of the Nature of Students’ Understandings about the Concept of Burning,” Journal of Research in Science Teaching 28 (1991): 689–704.
18. Rosalind Driver, “Beyond Appearances: The Conservation of Matter under Physical and Chemical Transformations,” in Children’s Ideas in Science, ed. Rosalind Driver, Edith Guesne, and Andrée Tiberghien (Milton Keynes, UK: Open University Press, 1985), 145–169.
19. Ichio Mori, Masao Kojima, and Tsutomu Deno, “A Child’s Forming the Concept of Speed,” Science Education 60 (1976): 521–529.
20. Lillian C. McDermott, Mark L. Rosenquist, and Emily H. van Zee, “Student Difficulties in Connecting Graphs and Physics: Examples from Kinematics,” American Journal of Physics 55 (1987): 503–513.
21. John Clement, “Students’ Preconceptions in Introductory Mechanics,” American Journal of Physics 50 (1982): 66–71.
22. Nella Grimellini Tomasini and Barbara Pecori Balandi, “Teaching Strategies and Children’s Science: An Experiment on Teaching about ‘Hot and Cold,’” in Proceedings of the Second International Seminar: Misconceptions and Educational Strategies in Science and Mathematics; July 26–29, 1987, ed. Joseph D. Novak (Ithaca, NY: Cornell University, 1987), 2:158–171.
23. H. W. Huang and Y. J. Chiu, “Students’ Conceptual Models about the Nature and Propagation of Light,” in Proceedings of the Third International Seminar on Misconceptions and Educational Strategies in Science and Mathematics, ed. Joseph D. Novak (Ithaca, NY: Cornell University, 1993).
24. R. Prüm, “How Do 12-Year-Olds Approach Simple Electric Circuits? A Microstudy on Learning Processes,” in Aspects of Understanding Electricity: Proceedings of an International Workshop, ed. Reinders Duit, Walter Jung, and Christoph von Rhöneck (Kiel, Germany: Institut für die Pädagogik der Naturwissenschaften, 1985), 227–234.
25. Vanessa Kind, “Pedagogical Content Knowledge in Science Education: Perspectives and Potential for Progress,” Studies in Science Education 45 (2009): 169–204.
26. Hunter McEwan and Barry Bull, “The Pedagogic Nature of Subject Matter Knowledge,” American Educational Research Journal 28 (1991): 316–334.
27. The term “Matthew effect” was coined by sociologist Robert Merton in 1968 and adapted to an education model by Keith Stanovich in 1986. See Robert K. Merton, “The Matthew Effect in Science,” Science 159, no. 3810 (January 5, 1968): 56–63; and Keith E. Stanovich, “Matthew Effects in Reading: Some Consequences of Individual Differences in the Acquisition of Literacy,” Reading Research Quarterly 21 (1986): 360–407.
28. Marilyn Jager Adams, Beginning to Read: Thinking and Learning about Print (Cambridge, MA: MIT Press, 1990).
[illustrations by James Yang]